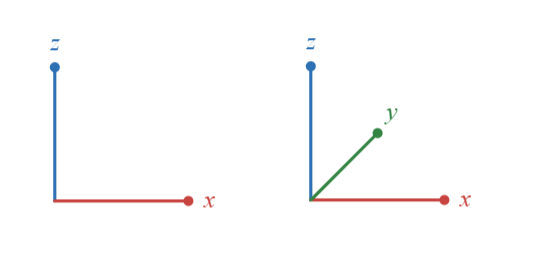透視投影とカメラ視点の準備

前回は、2Dキャンバスに3Dを表現するための基本――座標系や透視投影の原理を学びました。
今回は、Desmosグラフ計算機を使って「3Dらしさ」を描画する第一歩として、空間の投影準備とカメラ視点の考え方を扱います。

この記事は、第105話 【グラフ計算機／Desmos】 をテキスト化したものです。

🎯 目次

1. 描画用の座標系を定めなおす
2. カメラの視点と目線の定義
3. 視点からの透視投影
4. 次回に向けて

1. 描画用の座標系を定めなおす

右手系は右手系の中でも、次のように軸の向きを設定します。

• x軸：左右方向（従来通り）
• z軸：上下方向（数学的に縦軸として自然）
• y軸：奥行き方向（ZではなくYが奥に向かう）

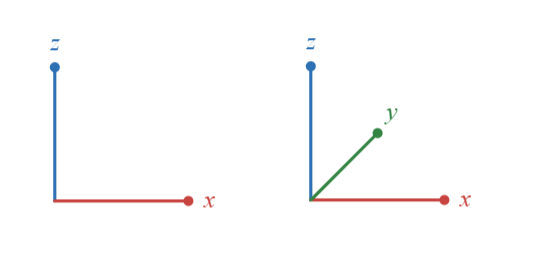
これは、xz平面 を基礎平面として扱うための工夫です。zが上、xが横、yが奥行きになります。

カメラが y軸方向（奥）に初めは向いていると仮定し、$(x,y,z)(x,\; y,\; z)$ を 2Dに投影する数式は以下の通りです：

$$(x^{\mathrm{\prime }},y^{\mathrm{\prime }})=(\frac{x}{y},\frac{z}{y})(x\text{'},\; y\text{'})\; =\; \backslash left(\backslash frac\{x\}\{y\},\; \backslash frac\{z\}\{y\}\backslash right)$$

$(x,y,z)(x,\; y,\; z)$は3D空間上の点、$(x^{\mathrm{\prime }},y^{\mathrm{\prime }})(x\text{'},\; y\text{'})$ はDesmosグラフ計算機上での投影位置です。遠く（$yy$が大きい）にあるほど、小さく描かれます。

2. カメラの視点と目線の定義

3D空間を見渡すためには、人間の目に相当する視点（カメラ位置）が必要です。カメラには以下の2つの情報が重要です。

• 位置ベクトル：カメラの位置 $P_{os}=(P_x,P_y,P_z)P\_\{os\}\; =\; (P\_x,\; P\_y,\; P\_z)$
• 回転（方向）：カメラの向いている方向（オイラー角） $R_{ot}=(R_x,R_y,R_z)R\_\{ot\}\; =\; (R\_x,\; R\_y,\; R\_z)$

オイラー角では、$x,y,zx,\; y,\; z$ 軸を中心とした回転です。

• $R_{x}R\_x$：ピッチ（上下回転）
• $R_{y}R\_y$：ヨー（左右回転）
• $R_{z}R\_z$：ロール（傾き）

3. 視点からの透視投影

カメラの位置を原点として3D空間を眺めるのが楽である。

Step1: カメラの位置とオブジェクト

そのため、「カメラを動かすこと」と「オブジェクトを動かすこと」の見かけの位置を下記のデモで観察すると、カメラを動かした方向と逆方向に動かせば見かけは同じである。

そのため、オブジェクトの位置を $o_{bj}=(x,y,z)o\_\{bj\}\; =\; (x,\; y,\; z)$ とするならば、見かけの位置は $o_{bj}-C_{am}o\_\{bj\}\; -\; C\_\{am\}$ といえる。

Step2: カメラの向きとオブジェクト

同様に、カメラの回転（向き）も少しトリッキーではあるが、カメラの向いた方向と逆方向に、カメラを中心に逆方向に動かせば見かけは同じである。

計算は大変であるが、$x,y,zx,\; y,\; z$軸の3軸すべてに回転を行う。
回転前の空間上の点 $p=(p_x,p_y,p_z)p\; =\; \backslash left(p\_x,\; p\_y,\; p\_z\backslash right)$ を、原点 $(0,0,0)\backslash left(0,0,0\backslash right)$ 中心に回転 $r=(r_x,r_y,r_z)r\; =\; \backslash left(r\_x,\; r\_y,\; r\_z\backslash right)$ させる関数 $r_{ot}r\_\{ot\}$ を定義する。

回転後の点 $p^{\mathrm{\prime }}=(x_2,y_2,z_2)p\text{'}\; =\; (x\_2,\; y\_2,\; z\_2)$ は次のように導ける。

以下は一つの関数としてまとめたものです。コピペして活用してください。

r_{ot}\left(p,r\right)=\left(\left(p.y\sin\left(r.z\right)+p.x\cos\left(r.z\right)\right)\cos\left(r.y\right)-p.z\sin\left(r.y\right),\left(\left(p.y\sin\left(r.z\right)+p.x\cos\left(r.z\right)\right)\sin\left(r.y\right)+p.z\cos\left(r.y\right)\right)\sin\left(r.x\right)+\left(p.y\cos\left(r.z\right)-p.x\sin\left(r.z\right)\right)\cos\left(r.x\right),\left(\left(p.y\sin\left(r.z\right)+p.x\cos\left(r.z\right)\right)\sin\left(r.y\right)+p.z\cos\left(r.y\right)\right)\cos\left(r.x\right)-\left(p.y\cos\left(r.z\right)-p.x\sin\left(r.z\right)\right)\sin\left(r.x\right)\right)

Step3: カメラ視点での透視図法

カメラの位置と向きをそれぞれ数式に落とし込むことができました。これらを合わせて、カメラの視点から見る3D空間上の点 $pp$ をグラフ計算機上の点を返す関数 $V_{iew}V\_\{iew\}$ は、

と表すことができる。3D to 2Dの描画は透視投影を用いています。

$p_{arse}p\_\{arse\}$ 関数の $(y>0)\backslash left(y\; >\; 0\backslash right)$ については、カメラ視点の裏側を描画しないために、制限をかけています。

4. 実践：グリッドを表示する

$V_{iew}V\_\{iew\}$ 関数を用い、$xyxy$ 平面にグリッドを表示します。

$$V_{iew}\left((t,\frac{[-5\dots 5]}{5},0)\right)(-1\le t\le 1)V_{iew}\left((\frac{[-5\dots 5]}{5},t,0)\right)(-1\le t\le 1)V\_\{iew\}\backslash left(\backslash left(t,\; \backslash frac\{\; \backslash left[-5\; \backslash ldots\; 5\; \backslash right]\}\{5\},\; 0\backslash right)\backslash right)\; \backslash \; \backslash left(-1\; \backslash le\; t\; \backslash le\; 1\backslash right)\backslash \backslash \; V\_\{iew\}\backslash left(\backslash left(\backslash frac\{\; \backslash left[-5\; \backslash ldots\; 5\; \backslash right]\}\{5\},\; t,\; 0\backslash right)\backslash right)\; \backslash left(-1\; \backslash le\; t\; \backslash le\; 1\backslash right)\backslash \backslash$$

カメラの移動はまだ実装していない（今後の記事に登場する）ので、雑に操作ができるデモを下に用意しました。

おわりに

今回は、カメラ（視点）と透視投影の原理を導入し、Desmos上で立体的に見える表現の土台を整えました。カメラの位置や向きを数式で操作することで、2D平面上でも3D空間を見渡すような描画が可能になります。

次回はこの仕組みを使って、木枠のようなワイヤーフレームの四角形（直方体）を3D空間に設置する方法を扱います。線と点を使って空間上に構造を組み立てることで、より実在感のある視覚表現に一歩近づきます。