2Dキャンバスで3Dを描く

2Dの平面上に、奥行きのある3D世界をどう表現するか――この疑問は、絵画や建築、コンピュータグラフィックスの分野で何世紀にもわたって追求されてきました。この記事では、ライブラリやツールを使わず、原始的な方法で3D空間を2Dに表現するための基本概念を学んでいきます。

この記事は、第104話 【グラフ計算機／Desmos】 をテキスト化したものです。

🎯 目次

1. 3D空間とは何か
2. 座標系の違い：右手系と左手系
3. 透視図法（パースペクティブ）の基本
4. 終わりに

---

1. 3D空間とは何か

3D空間は x, y, z の3つの軸で構成された座標空間です。

• x軸：左右（横方向）
• y軸：前後（奥行き）
• z軸：上下（縦方向）

これら3つの軸が交差して、立体的な位置を指定できるようになります。

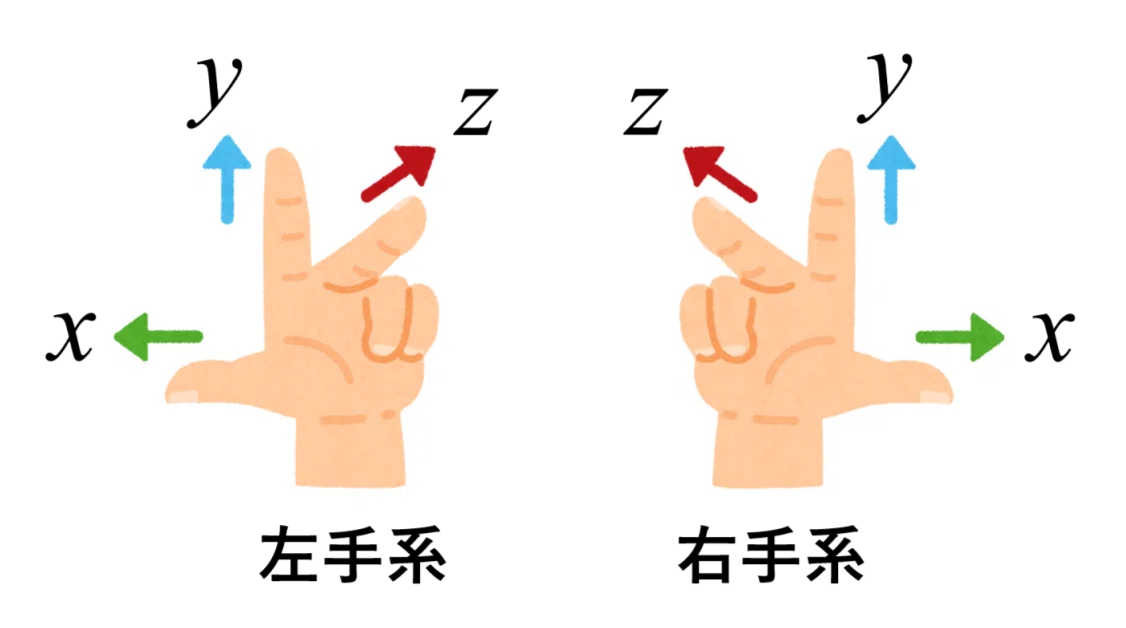
2. 座標系の違い：右手系と左手系

3D空間には、軸の向きとねじれの方向の違いにより、右手系と左手系の2つの座標系があります。

右手系（Right-handed coordinate system）

右手の親指、人差し指、中指を互いに直角に立てたとき：

• 親指：x軸
• 人差し指：y軸
• 中指：z軸
  これは多くの3Dグラフィックス（OpenGLなど）で採用されています。
  もちろん、数学の3Dグラフ計算機もこちらが採用されています。

左手系（Left-handed coordinate system）

左手を使って同様に指を立てると：

• 中指（z軸）が手前に向かいます。
  Unreal Engineなどで使われることがあります。

なぜ、このような座標系の違いが生まれたのか明確な理由があります。

3次元を作るにあたり、2次元の平面（xy平面）の基本の座標を考えます。

• x軸：左右（水平方向）
• y軸：上下（垂直方向）

ただし、次のように2つの流派があります

┼─→ x 　y　
│　　　　↑　
↓　　　　│　
y　　　　 ┼─→ x　　

左側はブラウン管やSVGキャンバス、緯度経度のような座標軸

• 右が正
• 下が正

右側は物理、数学でよく使われる座標軸

• 右が正
• 上が正

この別れた座標軸があることで、z軸を付け足したときに左手系、右手系が生まれるのです。（z軸は奥から手前に伸びる軸）

https://x.com/FreyaHolmer/status/1325556229410861056

今回は数学でよく使われる右手系を使用します。

3. 投影法の基本

投影法とは、3D空間の点を2D平面に写すためのルールです。
どの投影法も共通して、3Dの点 $(x,y,z)(x,\; y,\; z)$ を 2Dの点 $(x^{\mathrm{\prime }},y^{\mathrm{\prime }})(x\text{'},\; y\text{'})$ に変換 します。投影の方法がそれぞれ違うので、見え方が全く違います。

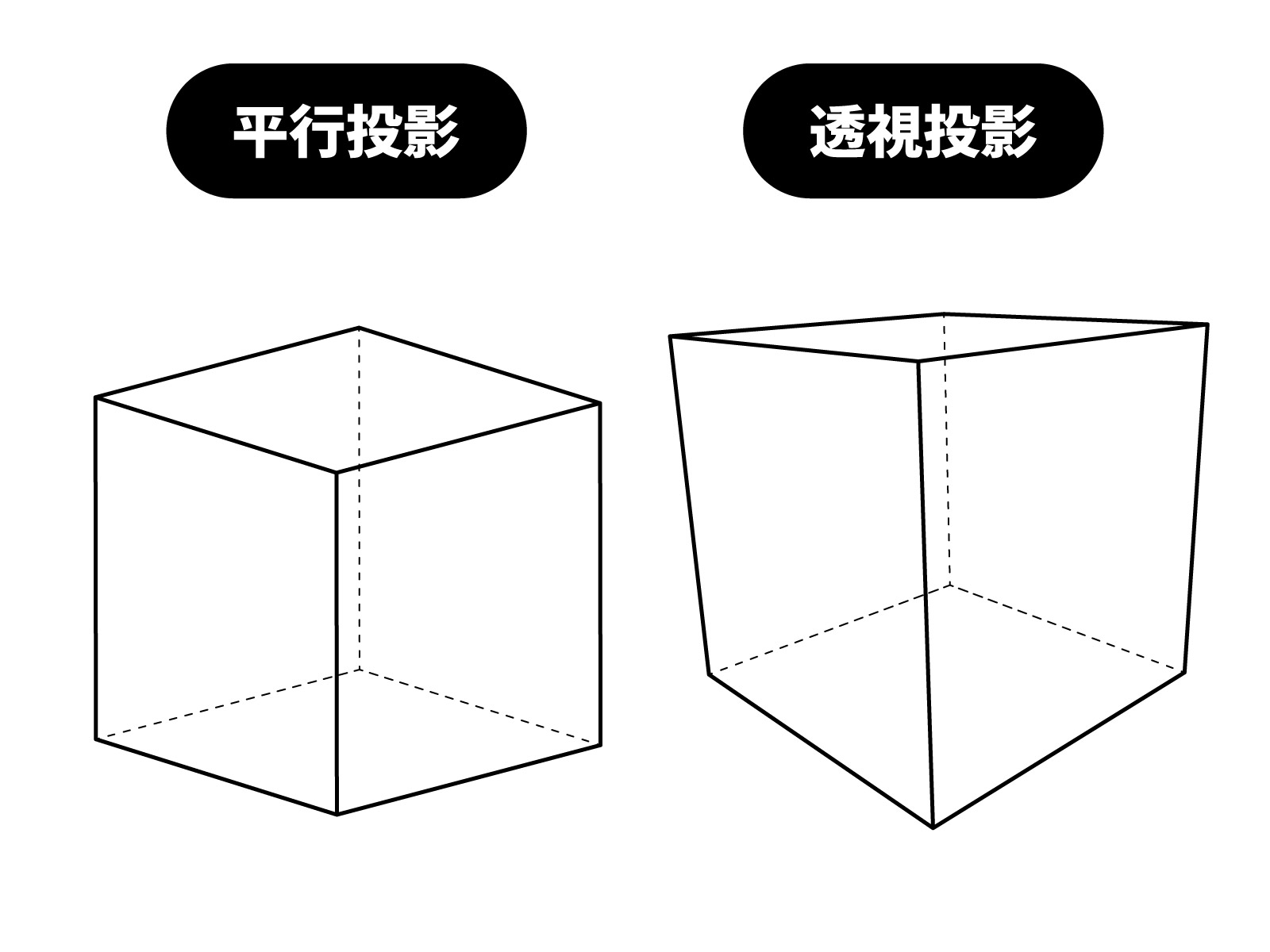
透視図法（Perspective Projection）

透視投影は、人間の目に最も近い写し方です。

特徴

• 遠くの物体は小さく、近くの物体は大きく見える
• 線が1点または複数の「消失点」に向かって収束する
• 空間の深さ・距離感が自然に表現できる

数学的な変換

$$(x^{\mathrm{\prime }},y^{\mathrm{\prime }})=(\frac{f\cdot x}{z},\frac{f\cdot y}{z})(x\text{'},\; y\text{'})\; =\; \backslash left(\backslash frac\{f\; \backslash cdot\; x\}\{z\},\; \backslash frac\{f\; \backslash cdot\; y\}\{z\}\backslash right)$$

$ff$：焦点距離（視点と画面の距離）
$zz$：奥行（カメラからの距離）
$zz$ が大きくなればなるほど、$1\mathrm{/}z1/z$は小さくなるので、物体が遠くにあればあるほど小さく見えるのです。

平行投影（Orthographic Projection）

平行投影は、寸法を正確に保ったまま写す方法です。

特徴

• 奥行き $zz$ に関係なく、物体の大きさは常に一定
• 線は平行のまま収束しない
• 建築設計図やCADなどで使用される

数学的な変換

$$(x^{\mathrm{\prime }},y^{\mathrm{\prime }})=(x,y)(x\text{'},\; y\text{'})\; =\; (x,\; y)$$

$zz$ は無視します。奥行きが存在しないように描かれるため、同じ大きさの物体が並んでいるように見えます。

魚眼投影（Fisheye Projection）

魚眼投影は、極端な視野を1枚の絵に収める特殊な投影です。

特徴

• 非線形な湾曲を伴う広角表現
• 中心からの角度によって歪みが発生
• 180° 以上の視野を1枚に収めることが可能

数学的な変換（例）

$$r=\sqrt{x^2+y^2},\theta =\frac{\arctan \left(\frac{r}{z}\right)}{r}(x^{\mathrm{\prime }},y^{\mathrm{\prime }})=(\frac{f\cdot \theta \cdot x}{z},\frac{f\cdot \theta \cdot y}{z})r\; =\; \backslash sqrt\{x^2\; +\; y^2\}\; ,\; \backslash \; \backslash theta\; =\; \backslash frac\{\backslash arctan\backslash left(\; \backslash frac\{r\}\{z\}\; \backslash right)\}\{r\}\; \backslash \backslash \; (x\text{'},\; y\text{'})\; =\; \backslash left(\backslash frac\{f\; \backslash cdot\; \backslash theta\; \backslash cdot\; x\}\{z\}\; ,\backslash frac\{\; f\; \backslash cdot\; \backslash theta\; \backslash cdot\; y\}\{z\}\backslash right)$$

$zz$ はカメラからの奥行き、$ff$ は画面上のスケーリング係数（焦点距離のようなもの）

立体感は感じることができますが、かなり歪んだ表現になるため正確な描画には適しません。

おわりに

私たちはスマホのような2Dの画面で、3Dモデルの立体表現を見ています。その裏側には奥行きある世界を描くための数学的・視覚的な工夫が詰まっています。まずはこの基礎をしっかりと身につけ、次のステップへ進んでいきましょう。